|
|
| | Fourieranalyse |
|
Der französische Mathematiker und Physiker Fourier hat herausgefunden, dass man jede periodische Funktion (also jeder ständig wiederkehrende Verlauf einer Kurvenform) in eine endlose Anzahl von Sinus-Schwingungen mit unterschiedlichen Frequenzen und Amplituden zerlegen kann. Die unterschiedlichen Frequenzen sind dabei ganzzahlige Vielfache der Funktionsfrequenz. Man nennt dieses Verfahren "Fourier-Analyse".
Geht man von einer Nicht-Sinusschwingung aus (ganz gleich, ob es eine Rechteckschwingung, eine Impulsschwingung o. ä. ist), so kann man durch die Fourier-Analyse die beteiligten Oberschwingungen ermitteln. Die erste sich daraus ergebende Schwingung ist die Grundschwingung.
Sie hat dieselbe Frequenz wie die Ausgangsschwingung (also die Nicht-Sinusschwingung). Alle weiteren Schwingungen -" also die Oberschwingungen dieser Ausgangsschwingung -" besitzen Frequenzen, die stets ganzzahlige Vielfache dieser Grundschwingung sind.
Mit Hilfe dieser so ermittelten Oberschwingungen kann man eine nicht sinusförmige Stromkurve oder Spannungskurve eindeutig beschreiben. Damit hat man gleichzeitig die Möglichkeit, die Auswirkungen von Stromverzerrungen oder auch Spannungsverzerrungen zu beschreiben.
Wird die Fourier-Analyse beispielsweise auf einen rechteckigen Wechselstrom (siehe Bild) angewandt, entstehen neben der Grundschwingung u. a. Oberschwingungen mit der 3- und 5-fachen Frequenz. Durch eine Addition aller Augenblickswerte der Grund- und sämtlicher beteiligter Oberschwingungen erhält man wieder die ursprüngliche Rechteckkurve. In der Abbildung fanden neben der Grundschwingung auch die 3. bis 17. harmonischen Oberschwingungen Berücksichtigung. Der Verlauf der Rechteckschwingung (blau) zeichnet sich bereits ab, ist aber noch nicht exakt zu sehen. Erst wenn sämtliche beteiligten Oberschwingungen addiert werden, ergibt sich der genaue Kurvenverlauf.
|
 |
Wendet man dieses Verfahren auf die Stromaufnahme eines B2-Gleichrichters an,
|
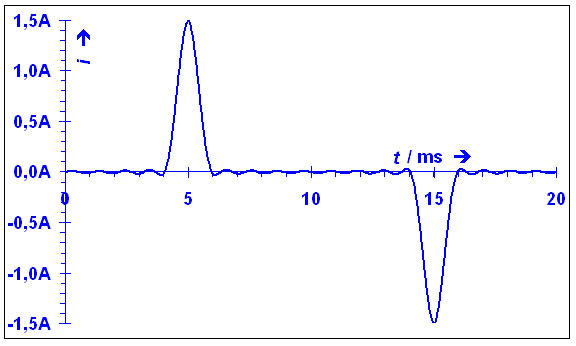 |
|
so entsteht das im nächsten Bild gezeigte Frequenz-Amplituden-Gemisch.
|
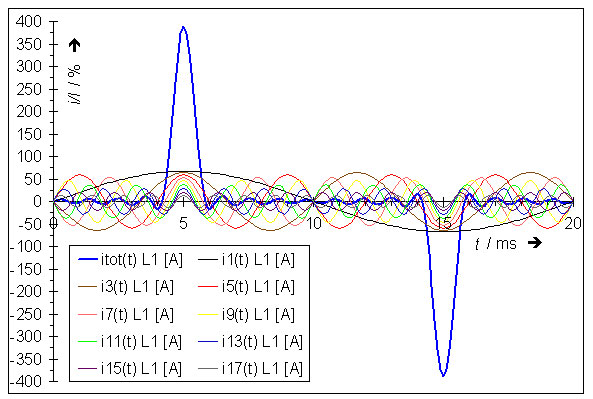 |
Zur einfacheren Beschreibung des Oberwellengehaltes stellt man das Vorhandensein und die Stärke der Oberschwingungen über ein Amplitudenspektrum dar. Beispielhaft sehen sie dazu das nächste Bild.
|
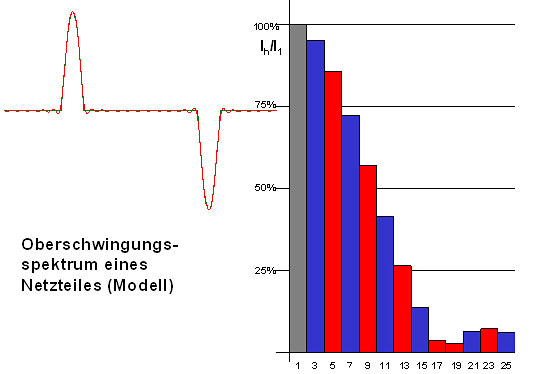 |
|
Derzeit auf dem Markt befindliche Messgeräte stellen die Analyseergebnisse als Balkenspektrum dar.
Die vorhandenen Stromoberschwingungen bewirken aufgrund von Netz- und Leitungsimpedanzen folgende Wirkungen auf die Netzspannung durch zusätzliche Spannungsfälle (Außenleiterspannung und Strangspannung, wie in folgenden Bildern zu sehen)
|
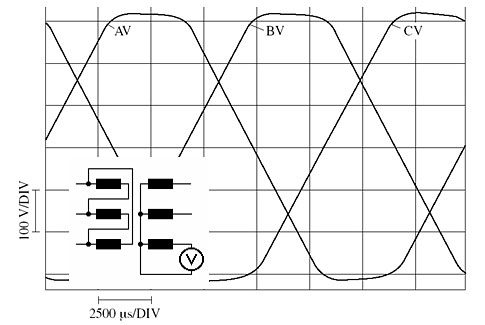 |
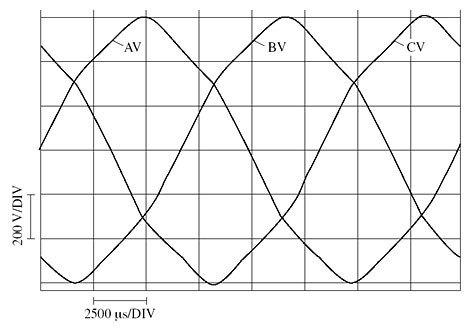 |
|
Verursacher solcher Verzerrungen sind alle Verbraucher, die eine nichtlineare Stromaufnahme hervorrufen, beispielsweise:
Stromrichter, Frequenzumrichter, Gleichstromsteller usw.
EDV-Anlagen mit USV (= unterbrechungsfreier Stromversorgung)
sämtliche Verbraucher mit elektronischen Netzteilen wie Computer, Drucker, Kopierer, Geräte der Unterhaltungselektronik, Haushaltsgeräte, E-lektronische Vorschaltgeräte (EVG) in der Beleuchtungstechnik u. a.
Mögliche Folgen dieser Verzerrungen:
Sie steigern insbesondere die Eisenverluste in Transformatoren; hier kann es zu einer thermischen Überlastung kommen.
Sie erhöhen den Blindleistungsanteil, da die Leistung, die Oberschwingungsströme hervorrufen, nicht effektiv genutzt werden können.
Sie beeinflussen die Abschaltcharakteristik von Leistungsschaltern; dies kann zu einer frühzeitigen Auslösung der Schutzeinrichtungen führen.
Sie bilden häufig eigene Drehfelder, die schneller umlaufen als das übliche Drehfeld der 50 Hz-Netzspannung. Außerdem können diese Oberschwingungs-Drehfelder zusätzlich zum Netzdrehfeld gegenläufig sein. Motoren, die durch das Drehfeld der Netzspannung angetrieben werden (z. B. Asynchronmotoren) werden dadurch beeinflusst, laufen unruhig, werden laut und überlastet (erhöhte Verluste).
Sie überlasten den Neutralleiter und können so zum Neutralleiterbruch führen, (vor allem durch die 3. harmonische Oberschwingung) hierdurch entstehen Brände bzw. konstant auftretende Überspannung bei angeschlossenen Betriebsmitteln.
Sie überlasten Kompensationsanlagen -" dabei wird die Verlustleistung in diesen Anlagen erhöht; auch in diesem Fall ist ein Anlagenausfall oder ein Brand zu befürchten.
Bei in der Anlage vorhandenen Kondensatoren (wie Kompensationsanlagen, Filter usw.) können sie zu Resonanzerscheinungen führen und so für Überspannungen sorgen.
Die Störwirkung des magnetischen Feldes von Oberschwingungsströmen ist wegen der höheren Frequenzen größer. Dadurch belasten sie zusätzlich die "elektromagnetische Umwelt" der übrigen Geräte und Anlagenteile.
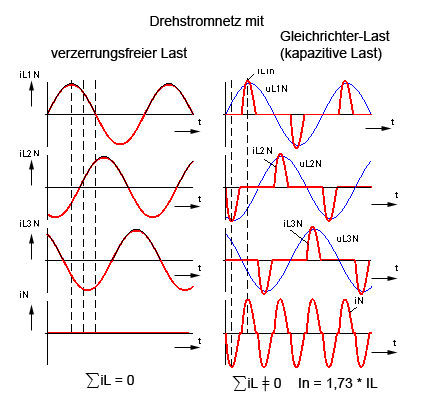
Bei dreiphasiger Belastung des Drehstromsystems mit jeweils gleich verteilten Gleichrichterlasten entsteht im Gegensatz zur klassischen Belastung des Drehstromnetzes folgendes:
Die Summation der Ströme im Sternpunkt (N-Leiter) würde im klassischen Fall zu einer Null-Stromstärke führen. Bei diesen speziellen Gleichrichterlasten führt es aber zu einer Summation der Außenleiterströme im Sternpunkt bzw. im N-Leiter. Diese Summation kann im schlechtesten Falle dazu führen, dass im N-Leiter das 1,73-fache des Außenleiterstromes auftritt. Der Neutralleiter wäre damit in aller Regel bei Nennstrom auf den Außenleitern überlastet (Bild ).
|
 |
|
Außerdem kommt es dabei zu kleinen Sternpunktverschiebungen, die das Drehspannungssystem in seiner Symmetrie verschieben. Eine Folge der N-Leiter-Überlastung wäre der N-Leiterbruch, der endgültig zu einer lastabhängigen Sternpunktverschiebung führt. Strangspannungen von 230 V im Normalfall können dann auf bis zu 390 V anwachsen (Bild )
|
 | |
|
| |